تابع محدب

تعریف

تابعی که در آن فضای بالای گراف تابع یک مجموعه محدب باشد. نمونه اولیه تابع محدب شکلی شبیه حرف "U" دارد. به عنوان مثال، توابع زیر نمونه‌هایی از تابع محدب هستند.

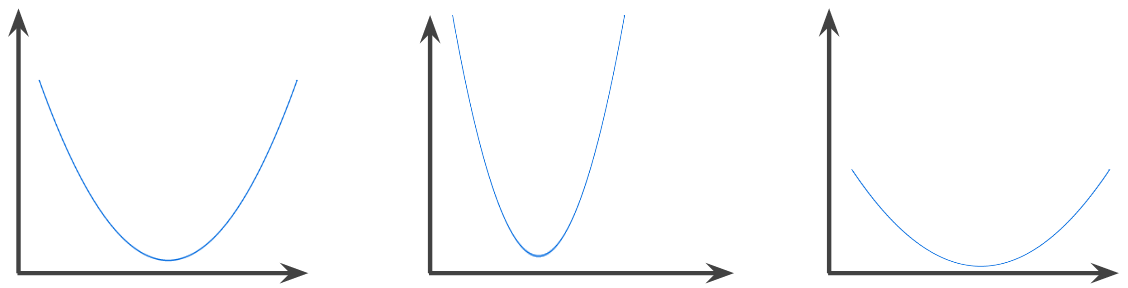
در مقابل نمودارهای فوق، توابع زیر محدب نیستند. توجه کنید که فضای بالای گراف یک مجموعه محدب نیست.

یک تابع اکیدا محدب دقیقا یک نقطه کمینه محلی دارد که همان نقطه کمینه سراسری است. توایع U شکل نیز جزو توایع اکیدا محدب هستند. با این حال، برخی از توایع محدب، مانند خط صاف، U شکل نیستند.

تعداد زیادی از توابع زیان (loss functions) از جمله موارد زیر تابع محدب هستند.

• تابع زیان ‌L2 (L2 loss)
• تابع زیان لگاریتمی (Log loss)
• تنظیم L1 (L1 regularization)
• تنظیم L2 (L2 regularization)

تعداد زیادی از انواع الگوریتم‌های گرادیان کاهشی (gradient descent) تضمین می‌کنند که نقطه‌ای نزدیک به کمینه تابع اکیدا محدب را پیدا می‌کنند. هم‌چنین، تعداد زیادی از انواع الگوریتم های گرادیان کاهشی تصادفی (stochastic gradient descent) نیز شانس بالایی در پیدا کردن نقطه‌ای نزدیک به کمینه یک تابع اکیدا محدب دارند.

مجموع دو تابع محدب (به عنوان مثال، تابع زیان L2 + تنظیم L1) نیز تابعی محدب است.

مدل‌های عمیق هرگز توابع محدب نخواهند بود. باید توجه داشت که الگوریتم‌هایی که برای بهینه‌سازی محدب (convex optimization) طراحی شده‌اند تلاش می‌کنند تا به هر روش پاسخی مناسب برای شبکه‌های عمیق پیدا کنند، اما این پاسخ لزوما مقدار کمینه سراسری نخواهد بود.